What is the Probability of Hitting a Jack-High Flop? 3/6/25
If a Texas Hold'em poker player looks down and sees a jack-high hand (J2,J3,...J10), they
should know the probability of seeing a jack high flop
(defined as Jxx where x is less than or equal to a J).

The probability of a Jack-high flop (including JJJ and JJx flops), given you have 2 hole cards (J2,J3,...,J10) is about 10.19%.
Naturally, as you go up in hole cards (Q-high, K-high) the probability of an x-high flop gets larger because there are less cards ranked above your hole cards. I wanted to calculate this same probability for other x-high hands, and come up with a way to estimate the probability of any X-high flop on the fly, to know the probability of making top pair.
The probability distribution for cards (5, 6, ..., K, A) is as follows:
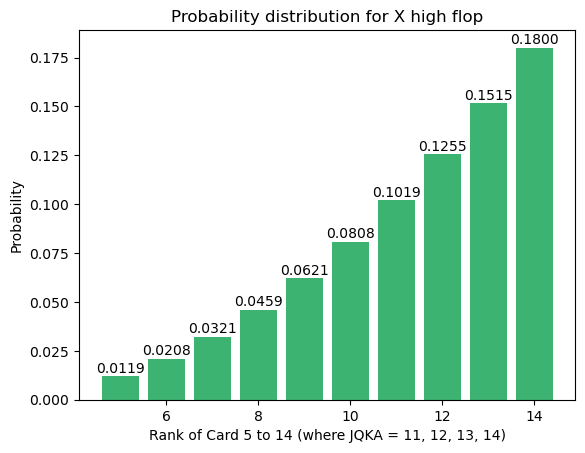
This means that, if you have a hand like 97, the probability you see a 9 high flop is about 6%. To come up with an easy way to calculate these probabilities, we take a look at the difference between each increase.
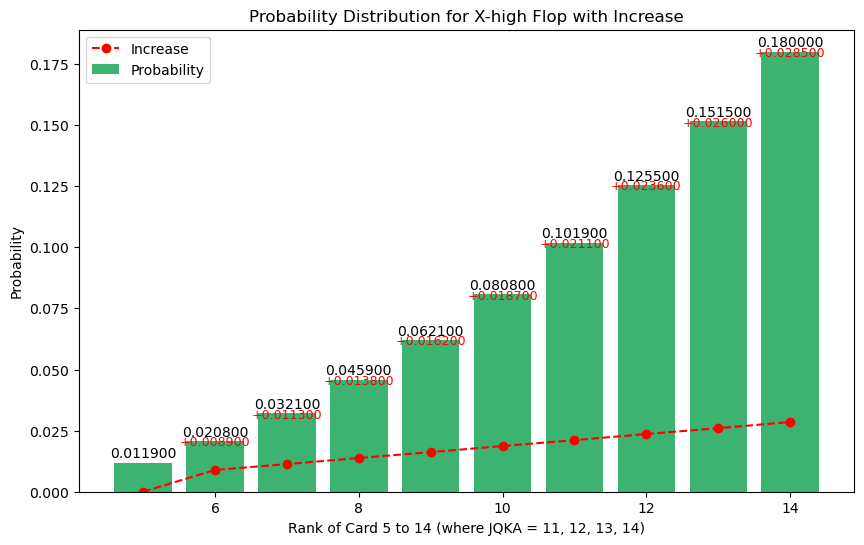
The increase rate (red line) shows a steady upward trend. My goal was to come up with a way to quickly estimate these values
for realistic poker scenarios such as Jack-high hands, so I started my estimation at card 9.
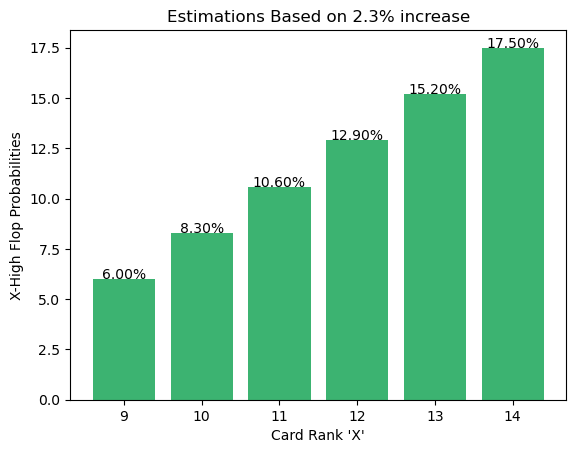
I've estimated the probabilities as follows:
If we let P(9 high flop) = 6%, we can increase each rank by
+2.3% on the fly to get a distribution very similar to the actual probability without memorizing every value:
To see more detail on these calculations, check out the jupyter notebook below.